速さと比は小6のツマヅキポイントです。
ブログ上でうまく書けるかは心配ですが、問題を解いてみたいと思います。
何かのお役にたてば…
問題を解く前に基本の確認です
速さの三用法は皆さんクリアしてますか?

面積図とともに覚えるようにしましょう。
距離=速さ×時間
速さ=距離÷時間
時間=距離÷速さ
図を意識しながら、比の合成をします。

上のように合成しましょう
次に、一定の値に注目
「距離一定のときだけ逆比」になります。
なぜなのかを考えることが重要です。丸暗記は禁物です。
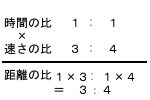
上のように、時間一定、速さ一定(1:1)のときは比が変わりません。(3:4のままですよね。他のも自分で試してみてくださいね)
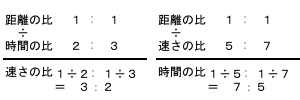
一方距離一定(1:1)のときは、割り算の式を考えるとお分かりのように、時間と速さの比は逆比になります。
上記の「比の合成」「一定の値」に注意しながら問題を精読します。
問題
100mを走るのにAは16秒、Bは20秒かかります。同じ方向に同時にスタートして100m走ったとき、Aがゴールすると、Bはゴール手前何mのところにいますか。
まず問題の前半部分「100mを走るのにAは16秒、Bは20秒かかります。」
ここで読み取りたいのは、距離一定です。
時間の比A:B=16:20=4:5
速さの比A:B=5:4(時間の比の逆比です。)
次に後半部分「同時にスタートして100m走ったとき、Aがゴールすると、Bはゴール手前何m」読み取ってほしいのは、時間一定です。
速さの比=5:4
距離の比=5:4(そのままです)
これを図にまとめると

⑤=100mだから
2人の差①=100×①/⑤=20m
もう一度ポイントを…
問題を読むときに「比の合成」「一定の値」に注意する。
お役に立ちましたか?