■どう無限級数を使うか?
問題をもう一度載せます。(大変申し訳ありません。和が3.966と書いてしまいましたが、3.996でした。)
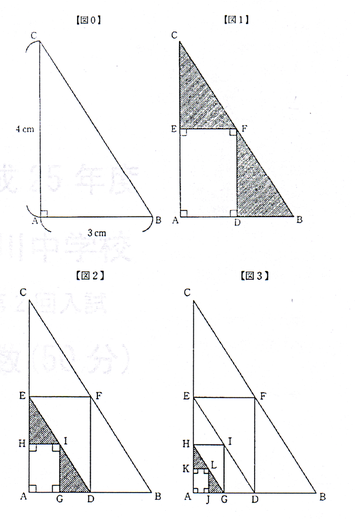
図1のようにAB,AC,BCの中点をそれぞれE,F,Gとします。このとき、三角形CEF,三角形FBDの面積の和を面積①と置きます。
図2、図3のようにこの作業を繰り返していきます。
(1) 省略
(2) 面積①+面積②+面積③+・・・と加えて
いくとき、初めて和が3.996を超えるのは何番目の面積まで加えたときか答えなさい。
市川中H25 第2回入試 より
ちなみに相似を使うと、
面積①は 3 です。面積②は 3/4 、面積③は 3/16、…
お気づきでしょうか?等比数列が出てきました。
和は、3 ×( 1 + 1/4 + 1/16 + …)= 3.996
となります。
両辺を3で割ると
1 + 1/4 + 1/16 + … =1.332
1/4 + 1/16 + … =0.332(前回の無限等比級数に似ている…というか、そのままの式ですよ!)
ここで、前回の正方形の登場です。
ここから手書きで失礼します。
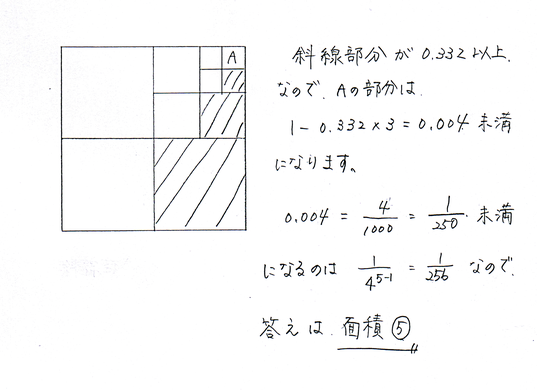
こんなに、綺麗に解答を導く必要はありません。実際、生徒たちは計算をひたすらやっていました。それでもいいんです。しかし、少しの工夫と知識でこんな解法も可能なんです!!難しいなんて言わないでくださいね・・・ただ、どうです?美しくないですか?
思いのたけをここにぶつけてもしょうがないので、このへんにして…
こういう問題を作る先生方、お疲れ様です。
今年はどんな入試問題に出会えるのでしょうか?楽しみです。受験生の皆さんも、あとひと踏ん張り。当日、入試を楽しめるくらい、今やるべきことにしっかり取り組みましょう。
今日はここまでにします。