みなさん、こんにちは。こんばんは。やのです。
本日は小5生の授業で音の話をしました。
その際、弦楽器の話になってですね・・・本物の琴を演奏したことがある生徒がいました。ちょっと興味が湧きますよね。「琴」を触ったこともないおじさんはちょっと羨ましく思いました。
昔から文人の教養は、琴棋書画って言われていて・・・ってどうでも良いですか??ちなみに「棋」は囲碁のことをいうのですよ(私、少々嗜んでおります。最近打てていませんが・汗)
閑話休題
それでは、昨日の問題を解いてみます。
ーーーーーーーーー
(1)1、2、3、4、5の5枚のカード並べて3桁の整数を作るとき、何通りの整数ができますか?
ーーーーーーーーー
この問題は樹形図の便利さを知ってもらう問題です。(手書きで失礼します。)

上図のように(全部は書いていませんが)樹形図を書くと、枝分かれの様子が同じことに気がつきます。かけ算を使って、
5×4×3=60
よって60通りの整数ができます。これはカンタンでしたね。
ーーーーーーーーー
(2)0、1、2、3、4の5枚のカードを並べて3桁の整数を作るとき、何通りの整数ができますか?
ーーーーーーーーー
これは、樹形図は条件のある項目から書き始めると良いことがわかる例題です。

図のように百の位に「0」のカードは使いないことを考えて樹形図をかくと、枝分かれの仕方は同じことに気がつきます。
4×4×3=48
よって48通りの整数ができます。これも解けましたね。
では、次の問題
ーーーーーーーーー
(3)0、1、1、2、3の5枚のカードを並べて3桁の整数を作るとき、何通りの整数ができますか?
ーーーーーーーーー
これはどうでしょう??
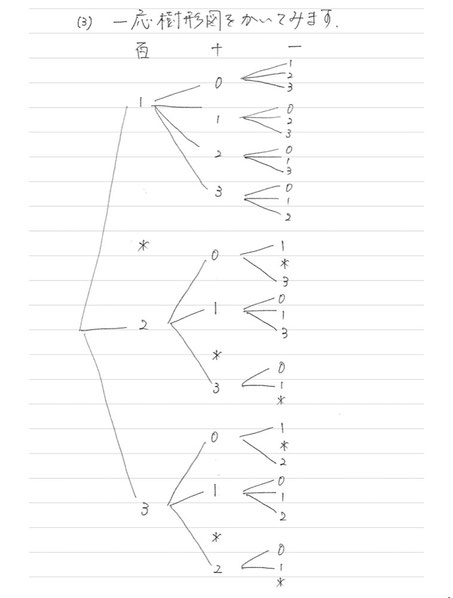
0のカード、同じ数字のダブりに気をつけながら丁寧にかいてみました(汗) 答えは26通りです。
この樹形図では、すべて書き出しただけで樹形図の利点である「かけ算(順列)を利用」することができません。答えは出せましたが、本当にこの解き方で良いのでしょうか?
この問題にはポイントがありまして・・・・・・・・
明日へ続きます。
本日はここまで。
また明日です。