みなさん、こんにちは。こんばんは。やのです。
本日は忘れ物をしてしまいました。いつも左腕につけているApple Watch。忘れるとその便利さを再認識できますね。
コンビニで支払いをしようと思い忘れてしまったことに気づいたおじさんでした。
時間を確認するのはもちろん、PCのロック解除や電子マネーでの支払い、その他通知の確認・・・全部ちょっとしたことなんですが、何回もやるとなると煩わしい。人間って楽することを覚えてしまうとダメですね(苦笑)
最短距離は垂線です。
閑話休題
昨日出題した問題を解いてみたいと思います。
それではお付き合いください。
ーーーーーーーーーーーーーー
H28 昭和秀英
ーーーーーーーーーーーーーー
ポイントは線分は点の集まりだと捉えて、中心と半径のチェクでした。
P・・・中心A、半径AB(最長)と半径AC(最短)
Q・・・中心B、半径BA(最長)と半径BC(最短)
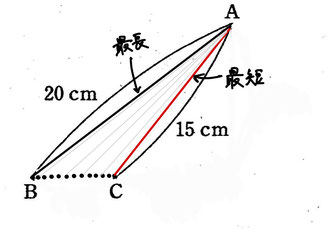
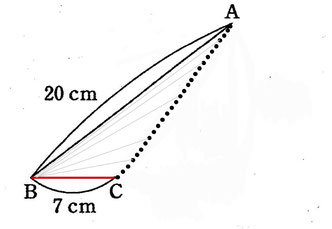
(1)
P=(20×20ー15×15)×3.14
Q=(20×20ー7×7)×3.14
より比をとれば良いので、×3.14は約分しまして
P:Q= 20×20ー15×15:20×20ー7×7 =175:351
ここまでは、問題ありません。しかし
R・・・中心C、半径CA(最長)と半径CB(最短)←これが問題です。
線分ABを点の集まりだと考えてください。そうするとCBよりも半径が短くなる点の存在に気づきます。
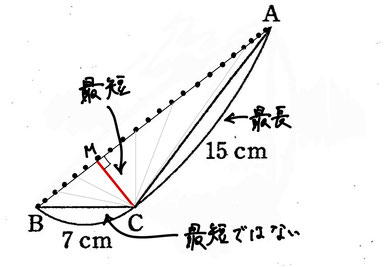
上図のように線分AB上に点Mをとると半径CMが最短となります。
(2)
CMを求めるには、長さを求めるときに利用できる手筋を思い出します。
相似・合同・二等辺三角形・面積比から逆算・面積から逆算・・・
たくさん授業で習ったことを思い出した中で、今回は「面積から逆算」を利用します。

三角形ABCは2通りの式で表せます。
底辺20cm、高さ⬜︎cmとみて、20×⬜︎÷2
底辺7cm、高さ12cmとみて、7×12÷2
この2つが等しいので、
⬜︎=4.2cm (逆算はお任せします)
あとは、(1)と同様に
Q:R= 20×20ー7×7 :15×15ー4.2×4.2(ここからの計算が厄介で、ユークリッドの互除法とか使うのですが今回は省略)
何やかんや計算しますと、
Q:R=325:192 となります。
いかがだったでしょうか?
半径をチェックするには、点の集まりとして図形を捉えるのがコツでした。
本日はここまで。
また明日です。
追伸
Googleマップさんのクチコミはこちらから投稿できます。よろしくお願いします。

