小5算数 通過算って簡単でしょ?
みなさん、おはこんばんちは
今日も独り言の更新です。
この2~3日とても寒いですよね。
寒さとは全く関係のない話ですが、本日は、水曜の小5生の授業の話をしたいと思います。
■単位付きの計算の意味
「通過算は情景図をかこう」と皆に伝えています。
授業では図をかいてもらってから、列車のすれ違いや、追い越しの問題を考えてもらいました。
みんな、旅人算の復習をよくやってくれていたようで、スラスラと解いていました。(なんだかうれしくなりました。)思わず「通過算って簡単でしょ」なんてみんなに言ってしまいました。
しかし、思いもよらないところでミスが出てきました。
速さの単位換算をせずに計算していたのです。
実は・・・このようなミスをしてもらいたくないので、速さの計算は単位付きでしてもらっていたのです。
みんな僕の「親心」受け止めてくれー
もう少し「慎重」になってくれー
・・・心の叫びでした。
このミスは冬期講習で取り返してもらおうと思っています。
もうすぐ、2015年が来ますね。1年が本当にあっという間に過ぎていきますね。
やり残しのないよう、日々精進していきます。
今日はここまでにします。
小5算数 平均の速さ
みなさんこんにちは。
と今まで書いてきましたが、いつごろ読んでいるのかわかりませんので…
みなさん、おはこんばんちは・・・ネタ元がわかる人は僕と同年代ですね。
今日は小5生の平均の速さについて少々…
■やはり図で解く
平均の速さを勉強しましたが、どのように解くのがいいのか
前回の授業で、速さの問題は「面積図を利用して解く」ことを徹底的に伝えました。
と言うことは・・・
平均の速さも面積図で解くんですね
比の分野で勉強した平均算が使えます。
メモをしながら問題を読んで、面積図にまとめながら考える。それを自分の言葉で説明してみる。
ここまでできれば、速さの問題は簡単になります。
この前の授業はダイヤグラムも学習しました。ダイヤグラムの話は後日…(以前もこのようなことを書いた記憶が…)
公式の丸暗記に頼ってしまうと、何を求めればよいかがわからず、適当に数字を合わせることをしてしまいます。
図を利用すれば、何がわからない(条件として与えられていない)から問題が先に進まないのか、必ず、自分なりに判断できるようになります。
この自分で判断することがどの科目にも必要となるスキルだと思っています。
算数だけにとどまらず、イロイロなことを自分で判断できるようになってほしいですね。
今日はここまでにします。
算数 速さの三用法
みなさん今日も独り言を書いていきます。
昨日の小5生の授業は「速さ」の単元に入りました。
■みはじ(きはじ)…図にして考えよう
速さの三用法と言えば、「みはじ」でしょうか?「きはじ」でしょうか?
僕はどちらも使っていません。授業では、面積図です。
算数 速さとは連想ゲーム
みなさん今日も独り言を書きます。
今日は、速さと比について思い付きで…
速さについてと言うよりは、頭の使い方を書きます。
お付き合いください。
本題に入る前になぜ今回のテーマは速さと比なのか?
最近ご相談が多い… ただこれだけです。
以前にも書いていますのでどうぞご参照ください。
比の合成・一定の値は見つかる様になっているでしょうか。
ダイヤグラムは丁寧に書けるようになっているでしょうか。
ダイヤグラムで相似が使えますか?どんな時相似を利用しますか?
距離一定の三角形は使えますか?
(後日ダイヤグラムまとめます…きっと…)
池の周りの旅人算はメモリの感覚がついているでしょうか。
通過算はどこに注目した方が楽でしょうか。
流水算速さの線分図……
頭の中にチェックポイントをいくつも用意しておくイメージです。
一つひとつ考えていくと初めは時間がかかります。
けれども、何度も何度も繰り返していくことによって、それこそヒラメクようになってきます。
条件の見え方(見つかり方)がきっと変わってくるはずです。
上に書いたように次々と連想することができるでしょうか。
頭の使い方は連想ゲームです。
「○○と言うことは→△△が考えられる。」を繰り返すことです。
これをすることによって、全ての条件を把握するのです!!
本日はここまでにします。
小6 速さと比 その2
速さと比は小6のツマヅキポイントです。
ブログ上でうまく書けるかは心配ですが、問題を解いてみたいと思います。
何かのお役にたてば…
問題を解く前に基本の確認です
速さの三用法は皆さんクリアしてますか?

面積図とともに覚えるようにしましょう。
距離=速さ×時間
速さ=距離÷時間
時間=距離÷速さ
図を意識しながら、比の合成をします。

上のように合成しましょう
次に、一定の値に注目
「距離一定のときだけ逆比」になります。
なぜなのかを考えることが重要です。丸暗記は禁物です。
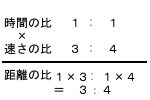
上のように、時間一定、速さ一定(1:1)のときは比が変わりません。(3:4のままですよね。他のも自分で試してみてくださいね)
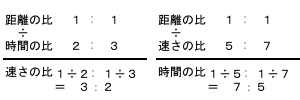
一方距離一定(1:1)のときは、割り算の式を考えるとお分かりのように、時間と速さの比は逆比になります。
上記の「比の合成」「一定の値」に注意しながら問題を精読します。
問題
100mを走るのにAは16秒、Bは20秒かかります。同じ方向に同時にスタートして100m走ったとき、Aがゴールすると、Bはゴール手前何mのところにいますか。
まず問題の前半部分「100mを走るのにAは16秒、Bは20秒かかります。」
ここで読み取りたいのは、距離一定です。
時間の比A:B=16:20=4:5
速さの比A:B=5:4(時間の比の逆比です。)
次に後半部分「同時にスタートして100m走ったとき、Aがゴールすると、Bはゴール手前何m」読み取ってほしいのは、時間一定です。
速さの比=5:4
距離の比=5:4(そのままです)
これを図にまとめると

⑤=100mだから
2人の差①=100×①/⑤=20m
もう一度ポイントを…
問題を読むときに「比の合成」「一定の値」に注意する。
お役に立ちましたか?
小6算数 速さと比
久しぶりの独り言です。
やはり、筆不精の性格が…
と言い訳はここまでにして、速さの話です。
実は3週間ほど前から、ベーシック(毎日解くプリント)にちょっとずつ出題してきたのですが、今日再びイントロダクションしました。
皆さんよく定着していました。
比の合成を狙いながら文章を「精読」する。
一定の値は何なのか考えながら「精読」する。
これだけです。
比の合成はいつも通り(比の文章題のとき同じ動き)に解く。
一定の値は「距離一定のときだけ逆比」ですね。
ダイヤグラムの使い方も少し話をしました。
「距離一定の三角形」
図形的に逆比を使いこなす方法です。
来週もう少し演習を積もうと思っています。
今週末は「志望校選定テスト」です。みんな頑張って!!
そういえば、今日の朝日小学生新聞に「金星の太陽面通過」の記事が載ってました。楽しみですね。
6/13 速さと比②更新しました
小6算数 速さと比
今日は速さと比の話です。
速さの問題は比が使えるようになると、格段に計算が楽になります。
ただし、抽象的すぎるのではじめは戸惑うことが多いですよね…
まずは比の合成を考えてみましょう。
次は一定の値に注目!
「○○一定は○○」をいちいち確認しましょう。
次回の速さと比はダイヤグラムを活用
今日の独り言はココまでです。